n 4n+1 *
2 2
1 5 2 + 1
2 2
3 13 3 + 2
2 2
4 17 4 + 1
2 2
7 29 5 + 2
2 2
9 37 6 + 1
2 2
11 41 4 + 5
2 2
13 53 7 + 2.
Otras gráficas, donde se visualiza de forma particular los resultados de la tabla anterior son las siguientes:
El cuadrado C de lado AD lo conforman 4 triángulos rectángulos, cuyas áreas son iguales a uno (1), además el triángulo ABD es congruente con cualquiera de los cuatros que forman parte del cuadrado C. Los catetos son los lados de dos cuadrados cuyas áreas son:
2 2
1 y 2.
La suma se escribe
2 2
1 + 2
que da como resultado el número primo 5. Es decir;
2 2
1 + 2 = 5,
que corresponde cuando n toma el valor de 1 en la expresión "4n+1".
De igual manera si n=3 la expresión anterior, se escribe:
2 2
3 + 2 = 13
y su gráfico es:
Otro ejemplo con la misma idea se consigue para n=4, así:
2 2
4 + 1 = 17 y 4(4) + 1 = 17.
Si generalizamos con estos resultados para cualquier triángulo rectángulo ABC y razonando con el siguiente gráfico:
En el cuadrado BCDE se observan cuatro triángulos congruentes al triángulo ABC, de donde se deduce la igualdad de áreas; así el área total del cuadrado BCDE podemos escribirlo como sigue:
En conclusión, de esta última igualdad se deduce que para todo número natural se tienen cuadrados consecutivos.
Ya en un artículo anterior se presentó el llamado Triángulo Pitagórico (TP), donde se observa una columna que tiene la siguiente sucesión de números naturales:
cuyo término general tiene la misma forma, es decir; son cuadrados consecutivos. Demostremos que cada elemento de esta sucesión expresa la forma conocida por EULER; escrita al comienzo del artículo, esta es:
4A + 1.
En efecto:





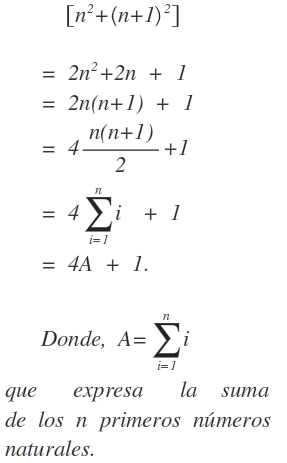
:)
ResponderEliminar