El conjunto N de los números naturales tiene un subconjunto bastante interesante, este es el conjunto de los números impares, cuyo término general tiene la forma 2k+1, donde k es cualquier entero, sin embargo tomaremos solamente los positivos mayores o iguales a uno. En tal sentido obtenemos la siguiente serie que llamaremos SI:
SI: 1, 3, 5, 7, 9, . . . , (2k+1).
Seguidamente se utiliza una fórmula presentada en el artículo "Una fórmula para los números cúbicos" escrito en este Blogger, la cual permitirá ordenar la base del Triángulo de naturales impares(TNI), en efecto; esta tiene la siguiente forma:
donde, fk es cualquier natural impar , por tanto; fk C SI.
Por consiguiente;
permite para todo n, calcular cada natural cúbico y observar cada sumando de la base del Triángulo de naturales impares; en otras palabras se obtienen cada uno de los elementos de la serie cúbica
y la suma de elementos impares que forman cada número cúbico.
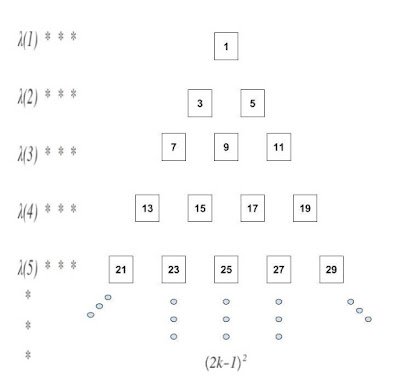
Ilustremos con un ejemplo lo afirmado en el párrafo anterior y luego la disposición final del Triángulo de naturales impares.




No hay comentarios:
Publicar un comentario