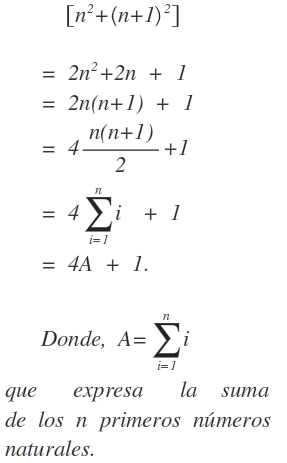ACERCA DE LA CONJETURA DE COLLATZ

     INTRODUCCIÓN

     Esta conjetura es un proceso, en el cual, al tomar cualquier número natural, este es sometido a varias operaciones, y de manera finita llegamos a 1. Las condiciones son las siguientes: Si el natural n es par(2k), este es dividido por 2 y si es impar(2k+1), se multiplica por 3 luego se le suma uno, con dicho resultado se repite el procedimiento hasta llegar a uno.

     Invito a los lectores a que aventuren a trabajar en la demostración de la conjetura, sólo deben probar que este proceso es finito y, que conduce a 1.

    Adelantaré algunos resultados comenzando con un diagrama general, un ejemplo particular, la prueba de que 3n+1 es par y, por último su relación con los números triangulares y los números cuadrados.

DIAGRAMA CONDUCTOR A 1

     A continuación propondré un esquema que contiene un procedimiento general para llegar a 1, para todo n perteneciente al conjunto de los números naturales. En efecto;

Ilustremos con un ejemplo particular, pero antes hemos llamado a fi como las diferentes operaciones a realizar, i = 1, 2, 3, ...:

      
     Seguidamente probaremos que 3n+1 siempre es un número par. En efecto; sea n=2k+1 y z=3n+1, para todo n∊N. Sustituyendo la primera igualdad en la segunda y realizando las operaciones pertinentes, se obtiene:

TRIÁNGULO DE NATURALES IMPARES

     El conjunto N de los números naturales tiene un subconjunto bastante interesante, este es el conjunto de los números impares, cuyo término general tiene la forma 2k+1, donde k es cualquier entero, sin embargo tomaremos solamente los positivos mayores o iguales a uno. En tal sentido obtenemos la siguiente serie que llamaremos SI:

                                                SI: 1, 3, 5, 7, 9, . . . , (2k+1).

      Seguidamente se utiliza una fórmula presentada en el artículo "Una fórmula para los números cúbicos" escrito en este Blogger, la cual permitirá ordenar la base del Triángulo de naturales impares(TNI), en efecto; esta tiene la siguiente forma:

donde, fk es cualquier natural impar , por tanto; fk C SI.

     Por consiguiente; 

permite para todo n, calcular cada natural cúbico y observar cada sumando de la base del Triángulo de naturales impares; en otras palabras se obtienen cada uno de los elementos de la serie cúbica

                   

y la suma de elementos impares que forman cada número cúbico.

     Ilustremos con un ejemplo lo afirmado en el párrafo anterior y luego la disposición final del Triángulo de naturales impares.

EL CERO Y EL INFINITO

     En eso de comparar segmentos surge algo interesante, que no es precisamente los números enteros, racionales ni irracionales.

      En efecto, tomemos un segmento unidad CD, cuyo módulo es igual a uno ( 1 ), es decir:

          En este sentido, se obtuvo la siguiente serie:

               La idea ahora es observar que forma tiene la suma de los términos de la serie anterior, es decir; utilizando símbolos de sumatoria, así tenemos que calcular la siguiente expresión:

por consiguiente, partiendo de la suma de los términos de la serie obtenida y realizando un pequeño cambio para un elemento mas se tiene:

          Finalmente, demostremos dos cosas;

                 1 que:

                                

, y

                 2 que:

        

           

EULER Y LOS NÚMEROS PRIMOS DE LA FORMA "4n + 1"

          Euler demostró que "Todo número primo de la forma 4n+1 puede expresarse de un modo único como la suma de dos cuadrados", observemos algunos en la siguiente tabla:

                                                    n                    4n+1                        *
                                                                                                      2         2
                                                    1                       5                    2     +   1

                                                                                                      2         2
                                                    3                      13                   3     +   2

                                                                                                      2         2
                                                    4                       17                  4     +   1

                                                                                                      2         2
                                                    7                       29                  5     +   2

                                                                                                      2         2
                                                    9                       37                  6     +    1

                                                                                                     2           2
                                                   11                      41                  4     +    5

                                                                                                     2           2
                                                   13                      53                  7     +    2.


          Otras gráficas, donde se visualiza de forma particular los resultados de la tabla anterior son las siguientes:

          El cuadrado C de lado AD lo conforman 4 triángulos rectángulos, cuyas áreas son iguales a uno (1), además el triángulo ABD es congruente con cualquiera de los cuatros que forman parte del cuadrado C. Los catetos son los lados de dos cuadrados cuyas áreas son:

                                                                          2            2
                                                                        1      y     2.

          La suma se escribe

                                                                          2            2
                                                                        1      +     2

que da como resultado el número primo 5. Es decir;

                                                                          2            2
                                                                        1      +    2    =   5,

que corresponde cuando n toma el valor de 1 en la expresión  "4n+1".

          De igual manera si  n=3  la expresión anterior, se escribe:

                                                                          2            2
                                                                        3       +   2    =   13

y su gráfico es:



                                                                 

          Otro ejemplo con la misma idea se consigue para  n=4, así:

                              2             2
                            4      +     1    =     17       y     4(4) + 1   =   17.

          Si generalizamos con estos resultados para cualquier triángulo rectángulo ABC y razonando con el siguiente gráfico:
                                                                   

          En el cuadrado BCDE se observan cuatro triángulos congruentes al triángulo ABC, de donde se deduce la igualdad de áreas; así el área total del cuadrado BCDE podemos escribirlo como sigue:

     En conclusión, de esta última igualdad se deduce que para todo número natural se tienen cuadrados consecutivos.

     Ya en un artículo anterior se presentó el llamado Triángulo Pitagórico (TP), donde se observa una columna que tiene la siguiente sucesión de números naturales:

                                

,

cuyo término general tiene la misma forma, es decir; son cuadrados consecutivos. Demostremos que cada elemento de esta sucesión expresa la forma conocida por EULER; escrita al comienzo del artículo, esta es:

                                                                    4A + 1.

     En efecto:

TRIÁNGULO PITAGÓRICO

           EL TRIÁNGULO ANTERIOR LO HE MENCIONADO VARIAS VECES EN EL ARTÍCULO ANTERIOR, EN TAL SENTIDO SÓLO LO PRESENTARÉ A MANERA DE EJEMPLO, MAS ADELANTE ESCRIBIRÉ UNAS PROPIEDADES BASTANTE INTERESANTES CON RESPECTO AL LLAMADO TRIÁNGULO PITAGÓRICO.