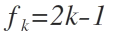TRES DESARROLLOS DISTINTOS CON EL MISMO RESULTADO

DESARROLLO NRO. 1

     En este apartado trabajaremos un poco con números cuadrados consecutivos. Llamaremos a cualquiera con el símbolo Cn, donde n es la base del cuadrado. Por ejemplo;  

     En tal sentido, evaluemos la siguiente expresión la que llamaremos Dn de forma general:

DESARROLLO NRO. 2

     En efecto: sea

   

     Esta función representa a los números impares como todos sabemos. Por otro lado, tenemos la suma de los n primeros números naturales expresada con la siguiente igualdad:

de la cual; llamaremos:

por lo que ahora podemos realizar la siguiente composición de funciones; 

Este resultado coincide con el anterior, por consiguiente, tenemos hasta ahora que:

DESARROLLO NRO. 3

     

     Finalmente con el tercer desarrollo, que no es mas que una representación de los números pares. Observemos la siguiente figura:

     Demostremos que efectivamente que 

.

     En efecto; los números pares están dados por:  2, 4, 6, 8, . . . , 2n, por tanto, la suma de los n primeros números pares lo calculamos de la siguiente manera:

 pero

luego; sustituyendo (2) en (1) y llamando T(n)  -  1, se tiene:

      

BIOGRAFÍAS BREVES

Leopold Kronecker 
(n. en Liegnitz actual Legnica en Polonia, 7 de diciembre de 1823 - † Berlín, Alemania,29 de diciembre de 1891).
En 1845 se doctoró en la Universidad de Berlín y en ese año escribió su disertación sobre teoría de números, dando una formulación especial a las unidades en ciertos campos numéricos algebraicos.
Matemático y lógico, Kronecker defendía que la aritmética y el análisis deben estar fundados en los números enteros prescindiendo de los irracionales e imaginarios. Fue autor de una frase muy conocida entre los matemáticos: "Dios hizo los números enteros; el resto es obra del hombre" (Bell 1986, p.477). 

Delta de Kronecker es una función de dos variables, que vale 1 si son iguales, y 0 si son diferentes. Se escribe con el símbolo ${\displaystyle \delta _{ij}\,\!}$ y se usa como una taquigrafía notacional más que como la función definida a trozos:

${\displaystyle \delta _{ij}=\left\{{\begin{matrix}1&{\mbox{si }}i=j\\0&{\mbox{si }}i\neq j\end{matrix}}\right.}$

PROFESOR JULIO ALBERTO PACHECO GERDEL

CHRISTIAN GOLDBACH

LEONHARD PAUL EULER

Charles Sanders Peirce 
(1839/09/10 - 1914/04/19)

Charles Sanders Peirce 

Filósofo y físico estadounidense 

Nació el 10 de septiembre de 1839 en Cambridge (Massachusetts). Hijo de Sarah y Benjamin Peirce, profesor de astronomía y matemáticas en Universidad Harvard.
Cursó estudios en la Universidad de Harvard. Entre 1864 y 1884 dio clases de lógica y filosofía en las universidades Johns Hopkins y Harvard, y en 1877 fue el primer delegado estadounidense en el Congreso Internacional Geodésico.
En 1861, realizó experimentos con péndulos que contribuyeron a la determinación de la densidad y forma de la Tierra, y también a desarrollar investigaciones sobre la dimensión de las ondas de luz. En 1867 se interesó por el sistema de lógica creado por el matemático británico George Boole, y trabajó hasta 1885 sobre la ampliación y transformación del álgebra de Boole.

LOTHAR COLLATZ

Lothar Collatz fue un matemático alemán. En 1937 propuso la conjetura de Collatz, la cual permanece sin ser resuelta. La fórmula Collatz-Wielandt para matrices positivas en el teorema de Perron-Frobenius es nombrada en su honor. Tomado de Wikipedia.

Fecha de nacimiento: 6 de julio de 1910,Arnsberg, Alemania

Fallecimiento: 26 de septiembre de 1990, Varna, Bulgaria

Campo: Matemáticas

Asesor académico: Erhard Schmidt

Alumno destacado: Frank Natterer

UN PATRÓN DE LOS NATURALES MULTIPLOS DE 3 EN EL TNI

     Se trata de otra propiedad bastante interesante sobre este Triángulo, el cual; describo a continuación:        
        Dada la siguiente figura:

observemos los naturales que están encerrados en los diferentes círculos de colores, estos aparecen cada tres bases según la siguiente serie(Los colores de los números coinciden con los de los círculos):

3, 6, 9, 12, . . . ,

cada elemento significa la cantidad de naturales múltiplos de 3 cada tres bases consecutivas en TNI, es decir; para λ(2), λ( 3) y λ( 4) tenemos el siguiente conjunto de números múltiplos de tres(3), 

{3, 9, 15 }

lo llamaremos A, por tanto; su cardinal es tres, es decir: #A = 3, así para λ(5), λ( 6) y λ( 7), se tiene otro conjunto que llamaremos B, 

B = {21, 27, 33, 39, 45, 51}

por consiguiente #B = 6. De manera similar , para  λ(8), λ(9) y λ(10), donde 

C = {57, 63, 69, 75, 81, 87, 93, 99, 105 } 

cuya cantidad de elementos está dado por la siguiente igualdad: #C = 9. 

     Seguidamente vamos a generalizar esta idea con la siguiente suma:

de ella nos interesa el Término general que se cumple para todo n mayor o igual a 1, recordemos que λ(1)=1, invito aplicar El Principio de inducción matemático para probarlo. Esta suma representa la suma de tres cubos consecutivos, esto es:

,

lo interesante de esta igualdad es el sumando λ(3n), que coincide con la suma de todos los múltiplos de 3 para cualquier n. Desarrollemos los ejemplos anteriores para aclarar mas esta propiedad. En efecto; para n = 1 se tiene:

.

     Para n = 2, 

     Y, para n = 3,

     En conclusión; el cubo central es la suma de todos los múltiplos de 3, esto se tiene cuando se toman tres bases consecutivas en el TNI.

  

LA SERIE DE CUADRADOS EN EL TRIÁNGULO DE NATURALES IMPARES Y SU ÍNDICE

     Ya anteriormente he escrito de manera general los diferentes números impares con el siguiente símbolo: 

.

     El índice se relaciona con tales números con la igualdad que presento seguidamente: 

la cual, es el término general de la serie 1, 3, 5, 7, 9, ... .

     Por otro lado, se realizó un arreglo que llamamos TNI (Triángulo de naturales impares), como lo índica la siguiente figura:

donde, se dedujo la relación mas simple de los números impares y su índice, esta relación la podemos entender de varias formas, a saber:

• Como una dupla: 

• Utilizando el símbolo "Si - entonces":

• En forma funcional: 

.

     Ahora podemos visualizar una serie, que geométrica-mente en el TNI representa la "altura", se trata se la serie: 1, 9, 25, 49, ... ; o, escrita utilizando el símbolo "fk" , como sigue: 

     La idea es encontrar la relación entre el índice y la primera serie. En efecto; comencemos por la serie que representan a los índices, esta es: 1, 5, 13, 25, . . ., los cuales se pueden escribir como sigue:

     Por tanto;

.

     De igual forma construimos el Término general de la serie:  1, 9, 25, 49, . . .; la cual, está dada por 

     Finalmente escribimos la relación buscada:

     También observando su patrón de formación:

MAS CERCA DE LA PRUEBA ABSOLUTA DE LA CONJETURA FUERTE DE GOLDBACH

     Comenzaré haciendo algunos comentarios sobre "El Triángulo de Naturales Impares (TNI)" que publiqué en un artículo anterior en este mismo Blogger, seguidamente probaré que los números cuyo término general es: 

pueden escribirse como la suma de dos números primos a través de la siguiente igualdad:

     En efecto, en el triángulo de números impares(TNI), están indicados los números impares positivos en orden creciente:

1, 3, 5, 7, 9, 11, . . .  .

     Escribiremos el primero como  f1 = 1, el segundo f2 = 3, el tercero con f3 = 5, etc., es decir, pongamos la serie así:

     La idea ahora es vincular el conjunto de los números impares con el índice, esto en una sola fórmula, es decir: 

,

para tal fin expresemos como sigue: f1 = 2.1 - 1, el segundo: f2 = 2.2 - 1, el tercero f3 = 2.3 - 1, generalizando para el n-ésimo número impar se tiene la fórmula buscada, la cual podemos probar con el "Método de inducción matemático", esta es:

.

     Por consiguiente, el TNI se visualiza de la siguiente forma:

     En consecuencia, se observan dos series numéricas que tienen las siguientes características:

luego, esto nos permite deducir los términos generales de los índices, los cuales están dados por:

     Por tanto; dichas series la escribimos como sigue:

   En tal sentido, unas de las implicaciones del TNI consiste en la construcción de la fórmula para números cúbicos, publicado en este mismo blogger, la cual tiene la siguiente forma:

donde;  representa los números impares componentes del TNI.

   Finalmente, demostremos a través de la última igualdad el objetivo planteado al comienzo, en efecto:

     Por otro lado, se puede dar el caso que no se obtiene directamente la suma de primos, pero para muchos casos existe un entero que llamaremos "j" que nos permite encontrar la suma deseada sin alterar la igualdad, por lo que la última igualdad la podemos escribir así:

  

con esto terminamos nuestra exposición.