Ya anteriormente he escrito de manera general los diferentes números impares con el siguiente símbolo:
El índice se relaciona con tales números con la igualdad que presento seguidamente:
la cual, es el término general de la serie 1, 3, 5, 7, 9, ... .
Por otro lado, se realizó un arreglo que llamamos TNI (Triángulo de naturales impares), como lo índica la siguiente figura:
donde, se dedujo la relación mas simple de los números impares y su índice, esta relación la podemos entender de varias formas, a saber:
- Como una dupla:
- Utilizando el símbolo "Si - entonces":
- En forma funcional:
Ahora podemos visualizar una serie, que geométrica-mente en el TNI representa la "altura", se trata se la serie: 1, 9, 25, 49, ... ; o, escrita utilizando el símbolo "fk" , como sigue:
La idea es encontrar la relación entre el índice y la primera serie. En efecto; comencemos por la serie que representan a los índices, esta es: 1, 5, 13, 25, . . ., los cuales se pueden escribir como sigue:
Por tanto;
De igual forma construimos el Término general de la serie: 1, 9, 25, 49, . . .; la cual, está dada por
Finalmente escribimos la relación buscada:
También observando su patrón de formación:

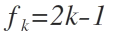









No hay comentarios:
Publicar un comentario