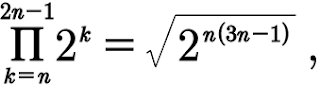ALTURA EN EL TRIÁNGULO DE PASCAL

                  Se trata de la sucesión de naturales 

                                      1, 2, 6, 20, 70, ...,

 la que llamaremos hTP y su término general hTP(n).

          En efecto; primeramente, visualizaré el "TRIÁNGULO DE PASCAL" y buscaré algunas características en su relación con los "TRIÁNGULOS DE NATURALES PARES E IMPARES", ya estudiados en artículos recientemente publicados:

          CARACTERÍSTICAS: 

1. Existe una simetría perfecta cuyo eje es hTP .
2. Visualizamos algunas sucasiones conocidas, tales como:

• 1, 1, 1, 1, . . .
• 1, 2, 3, 4, . . . n
• 1, 3, 6, 10, . . . n(n+1) / 2.                     

           3. Se observa que el término general de cada lateral es la suma de la sucesión anterior. Por ejemplo: 

                 4. Si seguimos con la misma idea, se tiene:

  

por tanto, se trata de la sucesión:

                                           1, 4, 10, 20, 35, . . . , n(n+1)(n+2) / 6, 

así:

por consiguiente, se trata de la sucesión:

                                           1, 6, 15, 35, 70, . . . , n(n+1)(n+2)(n+3) / 24 .

                   5. Continuemos con:

de donde se obtiene la sucesión:

                                          1, 6, 21, 56, 126, . . . , n(n+1)(n+2)(n+3)(n+4) / 120 .

          Ya con estas características se puede observar un patrón que describiré a continuación:

al observar los denominadores de la figura anterior nos percatamos de la sucesión:

                                                           1, 1, 2, 6, 24, 120, . . . ,

 o escrito en su forma factorial 

                                                           0!, 1!, 2!, 3!, 4!, 5!. . . . , 

cuyo término general es

                                                                    (n - 1)!

          Por otro lado, se puede construir y demostrar las siguientes igualdades con números combinatorios:

                                                                       

ahora bien, sustituyendo n por n+1 en la igualdad anterior obtenemos:

luego, el producto:

y, así, formar el patrón que nos da la fórmula o término general para la "ALTURA EN EL TRIÁNGULO DE PASCAL", la cual está dada por:

cuya sucesión está conformada por los naturales:

1, 2, 6, 20, 70, ...

FIN

SALTO ENÉSIMO EN PRODUCTOS DE POTENCIAS PARES E IMPARES

           Supongamos que tenemos la siguiente sucesión de potencias:

                                                                          

por un lado, el producto enésimo de dichas potencias está dado por: 

                                                             

la cual, establece la relación de los operadores del producto y la suma. Por otro lado, se observa en la GRÁFICA 1 y a través de los operadores una forma de llegar un poco mas allá de la potencia enésima; en efecto, supongamos que se agrega al producto enésimo un factor mas, en tal sentido se tiene la siguiente igualdad:

          Por consiguiente, se establecen las implicaciones:

   

GRÁFICA 1

   

           Ahora bien, si colocamos otro factor, luego de 2^(n+1), se observa la siguiente igualdad:

                Si continuamos con otro factor, se tendrá:

               Finalmente con este método el procedimiento nos conduce a los límites del operador pi y por ende a la fórmula general:

pero, si el exponente de la potencia es un número par (2k), se obtiene la igualdad:

y, si es impar (2k-1), el producto se transforma en:

Fin                 

RELACIÓN DE LOS OPERADORES PI Y SIGMA EN UNA SUCESIÓN DE POTENCIAS

           Dado el siguiente conjunto de potencias:

el cual, llamaremos A. Dicho conjunto se puede expresar de varias formas, las enumero a continuación:

          

          1.- {an}, el símbolo expresa una sucesión cuyo término general es 

          2.- Por extensión se determina colocando sus elementos entre lleves, esto se indicó en la parte inicial.

            3.- Se determina también indicando una propiedad que cumplen todos sus elementos, esto es 

 

 

en fin este tipo de expresión de conjuntos se llama por "Comprensión".

          4.- Existen formas gráficas que no mencionaremos, puesto que no es el objetivo de este artículo.

     

          A continuación formaré el producto de la enésima potencia y demostraré a través de algunas propiedades conocidas que se cumple la siguiente igualdad:

          Recordemos que debemos partir de un lado de la igualdad hasta llegar al otro lado utilizando técnicas de sustitución, esto lo haré con un discurso escrito. En tal sentido, partiendo del lado izquierdo de la igualdad, el mandato del operador  

me informa que debo colocar cada elemento de A en un producto, es decir;

luego, aplicando una de las propiedades de la potenciación, se tiene:

además, la suma enésima de los números naturales es igual a  n(n+1)/2, por tanto; 

esta última igualdad le podemos realizar las siguientes transformaciones:

    

.   Fin.

FÓRMULA GENERADORA DE PARES DE NÚMEROS PRIMOS

 INTRODUCCIÓN

     El presente escrito es sólo una descripción de una igualdad que genera pares de primos de la forma 2k^2 con k natural; es de notar, que a medida que aumentamos el valor de  n  se tienen números pares expresados como suma de dos números primos, me atrevo a asegurar que son infinitos, pero no son todos, mas adelante en otro artículo publicaré su demostración. Sólo haré un análisis de los elementos mas importantes, además del desarrollo de varios ejemplos particulares.

DESARROLLO 

         Se trata de la siguiente igualdad:

donde f es una forma funcional que establece una relación entre su sub-índice y los números impares, es decir; para todo n en el conjunto de los números naturales se tiene

 

          Con respecto al símbolo j, esta es una constante que permite establecer la igualdad entre los diferentes pares de naturales impares. Por ejemplo, sean a, b, c y d números impares:

      Si se cumple que a+b  =  c+d y todos diferentes, entonces    

     A continuación se desarrollan algunos ejemplos para visualizar la fórmula y así entenderla en su totalidad. En efecto:

EJEMPLO (1)

EJEMPLO (2)

USO DE LA FÓRMULA CÚBICA λ(n)

     Ya en varios artículos he mencionado por medio del símbolo λ(n) una igualdad que permite obtener los números cúbicos para un natural cualquiera, recordemos en este momento esta expresión, ésta es:

donde n pertenece a N y fi es un número impar. Con esta fórmula expresamos una de las propiedades del "Triángulo de números impares" del cual escribimos en el artículo: "TRIÁNGULO DE NATURALES IMPARES", pero lo que quiero señalar y es el objetivo de este nuevo artículo, es la demostración de la suma de los n primeros pares por medio de los números impares, el cual, está dado por

     En efecto; en primer lugar trataré de ilustrarla con la siguiente figura:

     La figura anterior resume de forma visual los elementos para el inicio de la demostración, estos son: los números impares (2n -1), la sucesión natural {n} y λ(n), por tanto; lo que queremos demostrar es:

Por consiguiente;

     Finalmente, con la propiedad de linealidad de la sumatoria, obtenemos lo que se quiere demostrar: