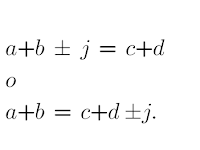RELACIÓN DE LOS OPERADORES PI Y SIGMA EN UNA SUCESIÓN DE POTENCIAS

           Dado el siguiente conjunto de potencias:

el cual, llamaremos A. Dicho conjunto se puede expresar de varias formas, las enumero a continuación:

          

          1.- {an}, el símbolo expresa una sucesión cuyo término general es 

          2.- Por extensión se determina colocando sus elementos entre lleves, esto se indicó en la parte inicial.

            3.- Se determina también indicando una propiedad que cumplen todos sus elementos, esto es 

 

 

en fin este tipo de expresión de conjuntos se llama por "Comprensión".

          4.- Existen formas gráficas que no mencionaremos, puesto que no es el objetivo de este artículo.

     

          A continuación formaré el producto de la enésima potencia y demostraré a través de algunas propiedades conocidas que se cumple la siguiente igualdad:

          Recordemos que debemos partir de un lado de la igualdad hasta llegar al otro lado utilizando técnicas de sustitución, esto lo haré con un discurso escrito. En tal sentido, partiendo del lado izquierdo de la igualdad, el mandato del operador  

me informa que debo colocar cada elemento de A en un producto, es decir;

luego, aplicando una de las propiedades de la potenciación, se tiene:

además, la suma enésima de los números naturales es igual a  n(n+1)/2, por tanto; 

esta última igualdad le podemos realizar las siguientes transformaciones:

    

.   Fin.

FÓRMULA GENERADORA DE PARES DE NÚMEROS PRIMOS

 INTRODUCCIÓN

     El presente escrito es sólo una descripción de una igualdad que genera pares de primos de la forma 2k^2 con k natural; es de notar, que a medida que aumentamos el valor de  n  se tienen números pares expresados como suma de dos números primos, me atrevo a asegurar que son infinitos, pero no son todos, mas adelante en otro artículo publicaré su demostración. Sólo haré un análisis de los elementos mas importantes, además del desarrollo de varios ejemplos particulares.

DESARROLLO 

         Se trata de la siguiente igualdad:

donde f es una forma funcional que establece una relación entre su sub-índice y los números impares, es decir; para todo n en el conjunto de los números naturales se tiene

 

          Con respecto al símbolo j, esta es una constante que permite establecer la igualdad entre los diferentes pares de naturales impares. Por ejemplo, sean a, b, c y d números impares:

      Si se cumple que a+b  =  c+d y todos diferentes, entonces    

     A continuación se desarrollan algunos ejemplos para visualizar la fórmula y así entenderla en su totalidad. En efecto:

EJEMPLO (1)

EJEMPLO (2)

USO DE LA FÓRMULA CÚBICA λ(n)

     Ya en varios artículos he mencionado por medio del símbolo λ(n) una igualdad que permite obtener los números cúbicos para un natural cualquiera, recordemos en este momento esta expresión, ésta es:

donde n pertenece a N y fi es un número impar. Con esta fórmula expresamos una de las propiedades del "Triángulo de números impares" del cual escribimos en el artículo: "TRIÁNGULO DE NATURALES IMPARES", pero lo que quiero señalar y es el objetivo de este nuevo artículo, es la demostración de la suma de los n primeros pares por medio de los números impares, el cual, está dado por

     En efecto; en primer lugar trataré de ilustrarla con la siguiente figura:

     La figura anterior resume de forma visual los elementos para el inicio de la demostración, estos son: los números impares (2n -1), la sucesión natural {n} y λ(n), por tanto; lo que queremos demostrar es:

Por consiguiente;

     Finalmente, con la propiedad de linealidad de la sumatoria, obtenemos lo que se quiere demostrar: 

FÓRMULA FACTORIAL PARA EL PRODUCTO DE NÚMEROS NATURALES CONSECUTIVOS

     Se trata del artículo: "CANTIDAD DE NÚMEROS NATURALES ENTRE CUBOS CONSECUTIVOS Y SU TÉRMINO GENERAL", en este concluímos que: 

     Esta última igualdad la tomaremos para deducir nuestra fórmula. Así, el producto de tres números naturales consecutivos lo podemos interpretar utilizando la definición de factorial de un número*, a continuación presento la siguiente tabla:

     Llamaremos f(n) al resultado obtenido, por lo tanto, afirmamos que con esta fórmula se calcula o se cuenta la cantidad de números naturales entre cubos consecutivos, es decir:

f(n) = (n+2)! / (n-1)!

     NOTA: *Factorial de n se simbiliza por  n! y significa o se define como:

n! = n.(n-1).(n-2) . . . hasta n factores, o sea,

n! = n.(n-1).(n-2).  . . .  . 3.2.1. 

     A continuación se observa una gráfica de la función obtenida, aclaro que deberíamos tener solamente puntos puesto que n pertenece a N, esta fue realizada con la APP GEOGEBRA.

CANTIDAD DE NATURALES ESTRE CUBOS CONSECUTIVOS Y SU TÉRMINO GENERAL

     Ya en una entrega anterior deducimos que la cantidad de números naturales esntre cuadrados consecutivos está dado por 2n. Es hora que nos preguntemos; ¿Qué forma tiene la cantidad de naturales entre cubos consecutivos?, antes daremos la siguiente definición: " Sea X una variable y #X la cantidad de naturales entre cubos consecutivos." 

     En efecto, se trata de la sucesión

                                                   1³, 2³, 3³, 4³, 5³, . . .

y, lo que queremos es calcular de forma general los diferentes valores que toma  X y contarlos entre  n³  y  (n+1)³, además del valor general de su suma.

     Así:

n³ < X < (n+1)³

     Si  n = 1, se tieene la siguiente inecuación,  1 <  X  <  8, cuyo conjunto solución es 

{2, 3, 4, 5, 6, 7},

el cual, llamaremos A1 , donde #X = 6. Utilizaremos la siguiente fórmula para obtener el número de elemento del conjunto, #X = an  -  a1  +  1, como se trata de un conjunto ordenado an es el último elemento y a1 es el primer elemento, asi para el caso del conjunto A1, an = 7 y a1 = 2. 

     Recordemos que sólo nos interesa son los valores de X o soluciones naturales de la inecuación para los diferentes valores que tomará n. 

     Ahora, si  n  =  2, obtenemos la siguiente inecuación  8  <  X  <  27, por tanto el conjunto solución es 

A2 = {9, 10, 11, 12, 13, 14, 15, . . . , 25, 26}, 

donde, #A2  =  26 - 9  +  1  =  18, el cual escribiremos  #A2  =  3  *  6.

     Seguidamente para n  =  3 se tiene la inecuación  27  <  X  <  64  y su conjunto solución es  

A3  = {28, 29, 39, .  .  .  , 62, 63}, 

donde  #A3  =  63 - 28  +  1 = 36 = 6 * 6.

     Hagamos para  n  =  4, y luego generalicemos para ir visualizando la forma que tiene el término general An. Por consiguiente, se tiene la inecuación  64  <  X  <  125 cuyas soluciones están dadas en el conjunto

A4 = {65, 66, 67,  .  .  .  , 124},

donde #A4  = 60, el cual podemos expresar asi:  A4  =  10 * 6, por tanto; ya realizado un análisis con estos resultados, vemos que se trata de patrones conocidos, si lo ordenamos como sigue:

#A1  =  1  *  6

#A2  =  3  *  6

#A3  =  6  *  6

#A4  =  10 * 6 

             *  *  *  *        

     *  *  *  *

          *  *  *  *     

#An  = [n(n+1)÷2]*6.

     Esta última igualdad nos señala la relación entre #An y la cantidad de naturales entre cubos consecutivos, la cual se puede expresar como sigue:

#An = 3n(n+1),

con otras palabras, si contamos los naturales entre cubos consecutivos el resultado es un natural multiplo de 3.

     Acontinuación probaremos que:

     En efecto;

        Por consiguiete;

  

.