Leopold Kronecker escribió en una oportunidad que "...el punto de partida de la matemática son los números naturales...", esto es cierto puesto que en la mayoría de los títulos que he desarrollado hay una premisa o mejor expresado, un axioma que no podemos pasar por alto, como lo es los números naturales y su suma. Estos son:
donde
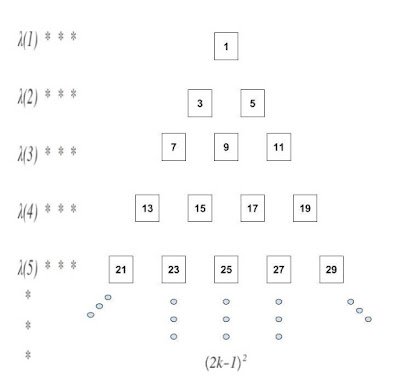
Por otro lado, con el estudio de la "Estructura plana de los números pares e impares", se utilizó un símbolo que permitió la simplificación del material de la exposición y una nueva forma de expresar la suma de los n primeros números naturales. Aparece en el apartado "3)" de la siguiente forma:
Mas adelante en dicho estudio se demostraron las siguientes propiedades:
Utilizaremos la primera " * " para llegar a la segunda " ** ". En efecto; ya se demostró que
donde Vn representa la suma de los n primeros números naturales, es decir
Así
Luego en la última igualdad, cambiando n por n - 1 se tiene:
de manera semejante
Sumando, resulta:
de inmediato podemos concluir que la suma de los n primeros números cúbico está dada por:
Finalmente se propone la demostración de la siguiente igualdad: